DDPMScheduler代码解释
class DDPMScheduler(SchedulerMixin, ConfigMixin):
"""
`DDPMScheduler` explores the connections between denoising score matching and Langevin dynamics sampling.
This model inherits from [`SchedulerMixin`] and [`ConfigMixin`]. Check the superclass documentation for the generic
methods the library implements for all schedulers such as loading and saving.
Args:
num_train_timesteps (`int`, defaults to 1000):
The number of diffusion steps to train the model.
beta_start (`float`, defaults to 0.0001):
The starting `beta` value of inference.
beta_end (`float`, defaults to 0.02):
The final `beta` value.
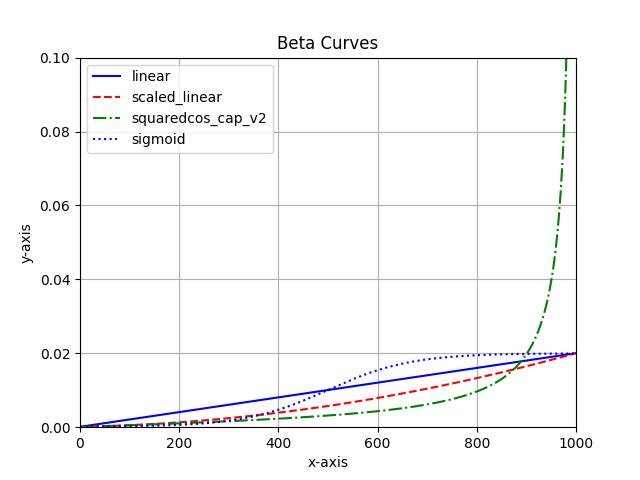
beta_schedule (`str`, defaults to `"linear"`):
The beta schedule, a mapping from a beta range to a sequence of betas for stepping the model. Choose from
`linear`, `scaled_linear`, or `squaredcos_cap_v2`.
trained_betas (`np.ndarray`, *optional*):
An array of betas to pass directly to the constructor without using `beta_start` and `beta_end`.
variance_type (`str`, defaults to `"fixed_small"`):
Clip the variance when adding noise to the denoised sample. Choose from `fixed_small`, `fixed_small_log`,
`fixed_large`, `fixed_large_log`, `learned` or `learned_range`.
clip_sample (`bool`, defaults to `True`):
Clip the predicted sample for numerical stability.
clip_sample_range (`float`, defaults to 1.0):
The maximum magnitude for sample clipping. Valid only when `clip_sample=True`.
prediction_type (`str`, defaults to `epsilon`, *optional*):
Prediction type of the scheduler function; can be `epsilon` (predicts the noise of the diffusion process),
`sample` (directly predicts the noisy sample`) or `v_prediction` (see section 2.4 of [Imagen
Video](https://imagen.research.google/video/paper.pdf) paper).
thresholding (`bool`, defaults to `False`):
Whether to use the "dynamic thresholding" method. This is unsuitable for latent-space diffusion models such
as Stable Diffusion.
dynamic_thresholding_ratio (`float`, defaults to 0.995):
The ratio for the dynamic thresholding method. Valid only when `thresholding=True`.
sample_max_value (`float`, defaults to 1.0):
The threshold value for dynamic thresholding. Valid only when `thresholding=True`.
timestep_spacing (`str`, defaults to `"leading"`):
The way the timesteps should be scaled. Refer to Table 2 of the [Common Diffusion Noise Schedules and
Sample Steps are Flawed](https://huggingface.co/papers/2305.08891) for more information.
steps_offset (`int`, defaults to 0):
An offset added to the inference steps. You can use a combination of `offset=1` and
`set_alpha_to_one=False` to make the last step use step 0 for the previous alpha product like in Stable
Diffusion.
rescale_betas_zero_snr (`bool`, defaults to `False`):
Whether to rescale the betas to have zero terminal SNR. This enables the model to generate very bright and
dark samples instead of limiting it to samples with medium brightness. Loosely related to
[`--offset_noise`](https://github.com/huggingface/diffusers/blob/74fd735eb073eb1d774b1ab4154a0876eb82f055/examples/dreambooth/train_dreambooth.py#L506).
"""
_compatibles = [e.name for e in KarrasDiffusionSchedulers]
order = 1
@register_to_config
def __init__(
self,
num_train_timesteps: int = 1000,
beta_start: float = 0.0001,
beta_end: float = 0.02,
beta_schedule: str = "linear",
trained_betas: Optional[Union[np.ndarray, List[float]]] = None,
variance_type: str = "fixed_small",
clip_sample: bool = True,
prediction_type: str = "epsilon",
thresholding: bool = False,
dynamic_thresholding_ratio: float = 0.995,
clip_sample_range: float = 1.0,
sample_max_value: float = 1.0,
timestep_spacing: str = "leading",
steps_offset: int = 0,
rescale_betas_zero_snr: int = False,
):
if trained_betas is not None:
self.betas = torch.tensor(trained_betas, dtype=torch.float32)
elif beta_schedule == "linear":
self.betas = torch.linspace(beta_start, beta_end, num_train_timesteps, dtype=torch.float32)
elif beta_schedule == "scaled_linear":
# this schedule is very specific to the latent diffusion model.
self.betas = torch.linspace(beta_start**0.5, beta_end**0.5, num_train_timesteps, dtype=torch.float32) ** 2
elif beta_schedule == "squaredcos_cap_v2":
# Glide cosine schedule
self.betas = betas_for_alpha_bar(num_train_timesteps)
elif beta_schedule == "sigmoid":
# GeoDiff sigmoid schedule
betas = torch.linspace(-6, 6, num_train_timesteps)
self.betas = torch.sigmoid(betas) * (beta_end - beta_start) + beta_start
else:
raise NotImplementedError(f"{beta_schedule} does is not implemented for {self.__class__}")
设 \( \bf x_0 \)表示一张图片, 逐步在当前图片上添加微小噪音,经过T步得到T张中间图片,依次为 \( \bf x_1, \bf x_2, \cdots, \bf
x_T \)。添加噪声的计算公式如下:
\( \bf x_t = \alpha_t \bf x_{t-1} + \beta_t \bf \epsilon_t \)
其中,
\( \bf \epsilon_t \sim \mathcal N(0,\mit I) \)
\( \alpha_t^2 + \beta_t^2 = 1, \alpha_t,\beta_t > 0 \)
为了实现每次添加噪音都很小,因此从标准正态分布取样,然后乘以一个很小的系数\( \beta_t \)就可以保证。
上面解释了为什么要设置\( \beta_t \)是一个很小的数字,取值范围限制在了[0.0001, 0.02]这个范围。
代码给出了beta序列的几种具体的取值方式。其取值如下图所示